-
C语言求自守数(详解版)
自守数是指一个数的平方的尾数等于该数自身的自然数。例如:
52 = 25 252 = 625 762 = 5776 93762 = 87909376
求100000以内的自守数。
问题分析
根据自守数的定义,求解本题的关键是知道当前所求自然数的位数,以及该数平方的尾数与被乘数、乘数之间的关系。
算法设计
若采用“求出一个数的平方后再截取最后相应位数”的方法显然是不可取的,因为计算机无法表示过大的整数。
分析手工方式下整数平方(乘法)的计算过程,以376为例:

本问题所关心的是积的最后三位。分析产生积的后三位的过程可以看出,在每一次的部分积中,并不是它的每一位都会对积的后三位产生影响。总结规律可以得到:在三位数乘法中,对积的后三位产生影响的部分积分别为:
- 第一个部分积中:被乘数最后三位×乘数的倒数第一位。
- 第二个部分积中:被乘数最后二位×乘数的倒数第二位。
- 第三个部分积中:被乘数最后一位×乘数的倒数第三位。
将以上的部分积的后三位求和后,截取后三位就是三位数乘积的后三位,这样的规律可以推广到同样问题的不同位数乘积中。
分离给定数中的最后几位
从一个两位数(存在变量n中)开始分析,分离最低位个位n%10;对于三位数n,分离最后两位n%100;对于四位数n,分离最后三位n%1000;...,由此可见,若分离出最后x位,只需要用原数对 10x 求余。
从第3部分所举例子可以看出,对于第二个部分积“2632”来说其实应是“26320”, 因为对于乘数中的倒数第二位“7”来说,因其在十位,对应的权值为10,第二个部分积实质上为:376X70=26320。故求部分积的程序段为:
int main () { //... while(k>0) { mul=( mul + ( number%(k*10) )*( number%b - nxuober%(b/10) ) )%a; /* (部分积+截取被乘数的后N位*截取乘数的第M位),%a再截取部分积*/ k /= 10; /*k为截取被乘数时的系数*/ b *= 10; } //... return 0; }对于整个循环来说,变量k是由number的位数确定截取数字进行乘法时的系数。第1次执行循环体时,被乘数的所有位数都影响到平方的尾数,因此第1个部分积=被乘数*乘数的最后一位,将部分积累加到变量mul上,再对a取余截取相应的尾数位数;第2次执行循环体,影响平方尾数的是被乘数中除了最高位之外的数(所以k先除以10再参加运算),第2个部分积=被乘数*乘数的倒数第二位,( number%b - number%(b/l0) )用来求乘数中影响平方尾数的对应位上的数;第3次、第4次执行循环体的过程同上。
程序流程图:
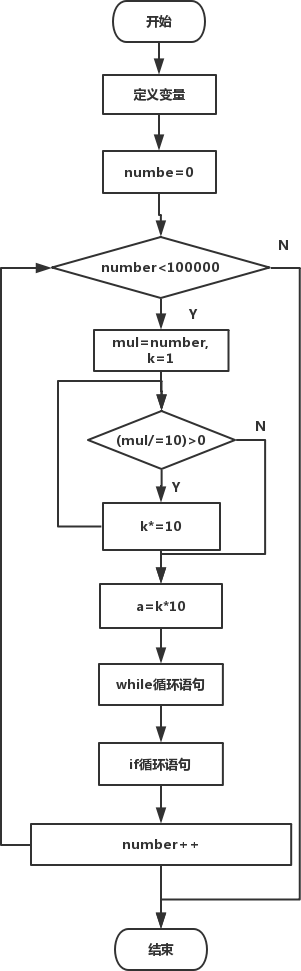
下面是完整的代码:
#include<stdio.h> int main() { long mul, number, k, a, b; printf("It exists following automorphic nmbers small than 100000:\n"); for( number=0; number<100000; number++ ) { for( mul=number, k=1; (mul/=10)>0; k*=10 ); /*由number的位数确定截取数字进行乘法时的系数k*/ a = k * 10; /*a为截取部分积时的系数*/ mul = 0; /*积的最后n位*/ b = 10; /*b为截取乘数相应位时的系数*/ while(k>0) { mul=( mul + ( number%(k*10) )*( number%b - number%(b/10) ) )%a; /*(部分积+截取被乘数的后N位*截取乘数的第M位),%a再截取部分积*/ k /= 10; /*k为截取被乘数时的系数*/ b *= 10; } if(number == mul) /*判定若为自守数则输出*/ printf("%ld ", number); } printf("\n"); return 0; }运行结果:
It exists following automorphic nmbers small than 100000:
0 1 5 6 25 76 376 625 9376 90625
更多...
加载中...