Peterson算法(解决临界区问题)详解
本节说明一个经典的基于软件的临界区问题的解决方案,称为 Peterson 算法。
Peterson 算法提供了解决临界区问题的一个很好的算法,并能说明满足互斥、进步、有限等待等要求的软件设计的复杂性。
Peterson算法适用于两个进程交错执行临界区与剩余区。两个进程为 P0 和 P1。为了方便,当使用 Pi 时,用 Pj 来表示另一个进程,即 j == 1 - i。
Peterson算法要求两个进程共享两个数据项:
int turn;
boolean flag[2];
变量 turn 表示哪个进程可以进入临界区。即如果 turn == i,那么进程 Pi 允许在临界区内执行。数组 flag 表示哪个进程准备进入临界区。例如,如果 flag[i] 为 true,那么进程 Pi 准备进入临界区。
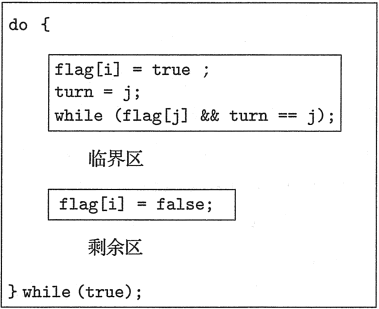
在解释了这些数据结构后,就可以分析如图 1 所示的算法。