C++ uniform_real_distribution连续均匀分布类模板用法详解
uniform_real_distribution 类模板定义了一个默认返回 double 型浮点值的连续分布。可以按如下方式生成一个返回值在范围 [0,10) 内的分布对象:
std::uniform_real_distribution<> values {0.0, 10.0};
std::random_device rd; // Non-de terrains tic seed source
std::default_random_engine rng {rd()}; // Create random number generator for(size_t i {}; i<8; ++i)
std::cout << std::fixed << std::setprecision(2)<< values (rng) <<" ";
// 8.37 6.72 6.41 6.08 6.89 6.10 9.75 4.07
生成和使用 uniform_real_distribution 函数对象的方式和 uniform_int_distribution 有密切的相似之处。可以将一个随机数生成器对象作为参数值给分布函数对象来获取一个随机值。可以通过调用对象的成员函数 pamm() 来获取和设置范围的界限。除了返回分布界限的成员函数 min() 和 max(),uniform_real_distribution 对象也有成员函数 a() 和 b()。注意,连续分布的范围是半开放的,分布对象返回值的范围不包括上边界。
现实世界中,能够应用均匀连续分布的变量是很少的。例如,和天气相关的参数的测量中,范围值并不是等可能性的。当我们看手表时,秒针的位置可能是一个均匀分布,但这没有什么用,这可能是真正的示例。均匀连续分布被用在应用于金融业的蒙特卡罗方法中,也被用到了工程和科学中。将它们放到一个使用连续均分分布或 π 的值程序。
使用连续均匀分布
你知道可以用一根木棍来确定 π 的值吗?当然,并不是让你用木棍来烕胁一个数学家,从而让他告诉你 π 的值,而是可以扔任意一根直的物品一铅笔甚至法拉克福香肠都可以。必须是一块光秃秃的带有地板的地面,并且扔的物品也必须是直的,它的长度必须小于地板的长度。过程很简单一只需要数扔木棍的次数,以及木棍落地时,它穿越地板边缘的次数。
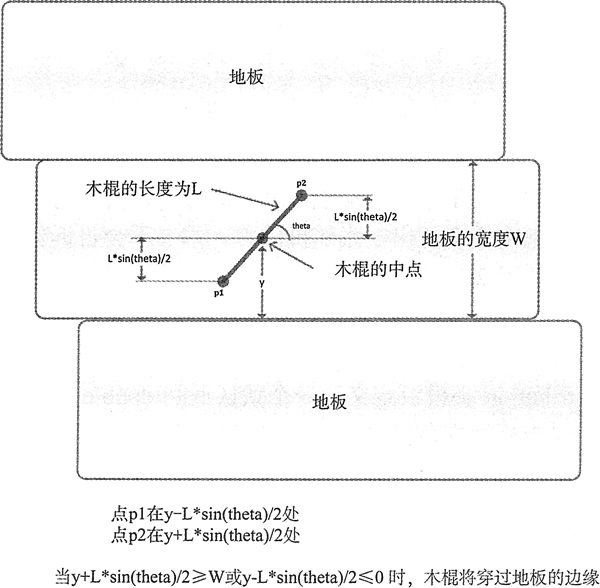
为了得到一个不错的结果,需要将棍子拋掷一定的次数。当然,这会花费一些时间,并且还有点乏味,并不是说有多累。在几组均匀分布的帮助下,我们可以通过电脑来模拟拋掷并计算处 π 的值。图 1 展示了木棍在地面上的随机位置以及它和地板的关系。为了解释发生了什么,需要用到一点数学知识,但并不难。