进制转换
所谓进制转换,就是将一种进制的数字转换为另一种进制的数字。数字的表示形式虽然改变了,但是数字的值并没有变。
这里我们讲解两种方法,第一种是简单的口算法,第二种是复杂的公式法。
进制转换口算法
我们来思考一个问题:为什么八进制数 17 对应的十进制数是 15?我们看八进制数 17 中的 7,这个 7 是没有进位的,它同十进制数 7 是一样的,因为它是在个位。而八进制数 17 中的 1,它能进一是因为有 8 才进一的,所以这个 1 代表的就是十进制的 8。所以一个 8 和一个 7 加起来就是 15,这就是为什么八进制数 17 对应的十进制数是 15 的原因。
现在我来考考读者,看读者能不能立刻回答出来。八进制数 23 对应的十进制数是多少?十进制数 34 对应的八进制数是多少?
同样,八进制数 23 中的 3 和十进制数 3 是一样的,而 2 说明进了两次位,有 8 才能进一次,进了两次说明是十进制的 16,所以 16 和 3 加起来就是 19。因此八进制数 23 对应的就是十进制数 19。
十进制数 34 里有 4 个 8,余 2,所以十进制数 34 对应的就是八进制的 42。
我再来问问大家,看大家能不能举一反三:十六进制的 3D 对应的十进制是多少?十进制的 83 对应的十六进制是多少?
方法是相同的,十六进制数 3D 中的 D 表示的是十进制的 13,而十六进制达到 16 才能进一次,数字 3 说明进了 3 次,即 48,13 和 48 加起来就是 61。因此,十六进制数 3D 就对应十进制数 61。同样,十进制 83 中有 5 个 16,余 3,所以十进制数 83 就是十六进制数 53。
如果是八进制和十六进制相互转换的话,因为它们都跟十进制有关系,所以可以将十进制当作一个桥梁,先转换成十进制,然后再转换成另一个进制。
以上的口算方法实际上就是进制转换的本质和奥秘的总结。但是用口算方法只能计算比较小的数字,当数字比较大的时候还是得在纸上算。之所以没有讲如何用口算进行二进制转换,原因就是二进制的计算量很大,不适合口算。介绍口算方法的主要目的是想让大家体会进制转换的本质,从而能够深刻理解下面所讲的公式法。
进制转换公式法
以上讲的是进制转换的本质,下面系统地讲一下进制转换。在阅读本节之前建议大家先掌握上节的内容,这样效率会更高,理解会更深刻。
1) r 进制转换成十进制
r 进制数 an an–1…a1 a0 对应的十进制数为:
an×rn + an–1×rn–1 + … + a1×r1 + a0×r0
下面给大家举几个例子:
- (1011011)2=1×26+0×25+1×24+1×23+0×22+1×21+1×20=64+0+16+8+0+2+1=91
- (356)8=3×82+5×81+6×80=192+40+6=238
- (2FB)16=2×162+15×161+11×160=512+240+11=763
2) 十进制转换成 r 进制
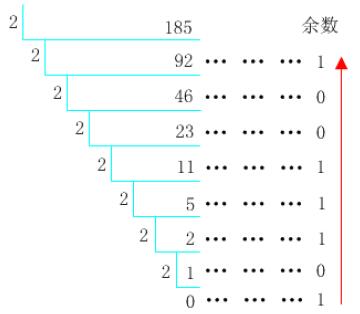
方法:除 r 取余数,直至商为零,余数倒序排序。
下面给大家举个例子:十进制 185 分别转换成二进制、八进制和十六进制。