返回
2022年06月21日
-
C语言求亲密数(详解版)
问题描述
如果整数A的全部因子(包括1,不包括A本身)之和等于B;且整数B的全部因子(包括1,不包括B本身)之和等于A,则将整数A和B称为亲密数。求3000以内的全部亲密数。
问题分析
根据问题描述,该问题可以转化为:给定整数A,判断A是否有亲密数。
为解决该问题,首先定义变量a,并为其赋初值为某个整数。则按照亲密数定义,要判断a中存放的整数是否有亲密数,只要计算出该整数的全部因子的累加和,并将该累加和存放到另一个变量b中,此时b中存放的也是一个整数。再计算b中存放整数的全部因子的累加和,将该累加和存放到变量n中。
若n等于a则可判定变量a和b中所存放的整数是亲密数。
算法设计
计算数A的各因子的算法:用A依次对i(i的范围可以是1〜A-1、1〜(A/2-1)中之一) 进行模(“%”,在编程过程中一定注意求模符号两边参加运算的数据必须为整数)运算,若模运算结果等于0,则i为A的一个因子加;否则i就不是A的因子。将所求得的因子累到变量B。
接下来求变量B的因子:算法同上,将B的因子之和累加到变量n。根据亲密数的定义判断变量n是否等于变量A(if(n==a)),若相等,则A和B是一对亲密数,反之则不是。
程序流程图:
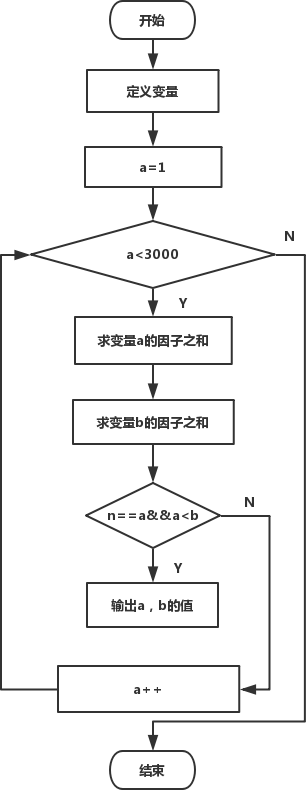
下面是完整的代码:
#include<stdio.h> int main() { int a, i, b, n; printf("There are following friendly--numbers pair smaller than 3000:\n"); for( a=1; a<3000; a++ ) /*穷举3000以内的全部整数*/ { for( b=0, i=1; i<=a/2; i++) /*计算数a的各因子,各因子之和存放于b*/ if(!(a%i)) b+=i; for( n=0, i=1; i<=b/2; i++ ) /*计算b的各因子,各因子之和存于n*/ if(!(b%i)) n+=i; if(n==a && a<b) /*使每对亲密数只输出一次*/ printf("%4d--%4d ", a, b); /*若n=a,则a和b是一对亲密数,输出*/ } return 0; }运行结果:
There are following friendly--numbers pair smaller than 3000:
220-- 284 1184--1210 2620--2924知识点补充
对于这类多次将某些值存储到一个变量中时,一定要注意变量赋初值的位置。
更多...
加载中...