-
概率、分布和熵及其概述
生成随机数隐隐包含着统计学的一些概念,下面会对它们进行概述。本节只是为了让你熟悉这些概念,并且应该足以使你明白本章的其他内容,即使你可能从来没接触过这些概念。
什么是概率
概率的值在 0 和 1 之间,它可以衡量事件发生的可能性。0 说明事件永远不会发生,1 说明事件肯定会发生。投一次骰子得到 6 的概率,或者实际上得到任何可能值的概率,都是 1/6。得到任意数字的概率是 1。
通常,事件发生的概率是它发生的次数除以它可能发生的次数。如果事件发生的概率是 p,那么它不发生的概率为 1-p。这样就为生活提供了宝贵指导。例如,在英国买彩票中奖的概率,从 49 个数中选取 6 个数,大约是 1/14 000 000;这意味着不中的概率大约为 13 999 999/ 14 000 000,基本是不可能中奖的。从这个角度来说,被闪电击中的概率是中彩票的 10 倍。
什么是分布
分布描述的是假设变量为序列中某个特定值的可能性。分布可以是离散或连续的:
离散分布描述的是假设变量是一组固定值中任意一个值的概率。根据定义,整数值的分布就是离散分布。用一个变量来表示投一次骰子的结果就是一个典型的离散分布的示例,它只能是从 1 到 6 的整数值。在离散分布中,所有可能值的概率之和为 1。
连续分布表示的是假设连续变量是序列中某个特定值的概率。连续变量可以是序列中的任意一个值,一天中某个给定时间的温度就是一个示例。
用来表示一个连续随机变量在某个范围内的值的概率的曲线被叫作概率密度函数 (Probability Density Function, PDF)。变量为给定值时,概率是点在 PDF 上对应的值。假设变量为 a 到 b 之间的任意值,变量的概率就是 a 到 b 之间的 PDF 曲线下方的面积。这意味着在 a 到 b 之间的 PDF 曲线下方的面积必须是 1,因为变量总为这个范围内的一个可能值。
离散变量的 PDF 被叫作离散概率函数。离散变量的不同值的概率通常使用图形的一套点或竖条来表示。像之前所说的那样,概率之和加起来必须为 1。
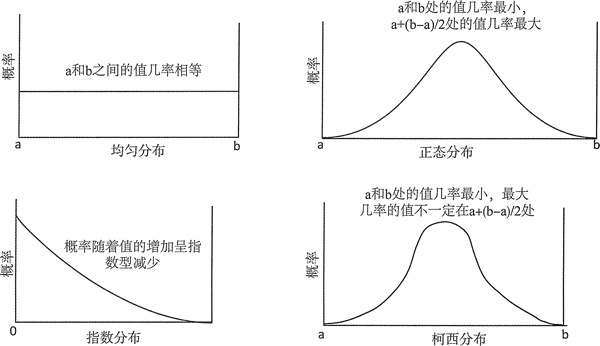
在现实世界中,有很多用来模型化事件是如何发生或如何测量的分布。它们通常被描述为数学公式,当以图形的形式展示时,就可以很容易地理解它们。图 1 展示了 4 个分布的示例。