-
汇编语言递归及应用详解[附带实例]
递归子程序(recursive subrountine)是指直接或间接调用自身的子程序。递归,调用递归子程序的做法,在处理具有重复模式的数据结构时,它是一个强大的工具。例如链表和各种类型的连接图,这些情况下,程序都需要追踪其路径。
无限递归
子程序对自身的调用是递归中最显而易见的类型。例如,下面的程序包含一个名为 Endless 的过程,它不间断地重复调用自身:
;无限递归 (Endless, asm) INCLUDE Irvine32.inc .data endlessStr BYTE "This recursion never stops",0 .code main PROC call Endless exit main ENDP Endless PROC mov edx,OFFSET endlessStr call WriteString call Endless ret ;从不执行 Endless ENDP END main当然,这个例子没有任何实用价值。每次过程调用自身时,它会占用 4 字节的堆栈空间让 CALL 指令将返回地址入栈。RET 指令永远不会被执行,仅当堆栈溢出时,程序终止。
递归求和
实用的递归子程序总是包含终止条件。当终止条件为真时,随着程序执行所有挂起的 RET 指令,堆栈展开。举例说明,考虑一个名为 CalcSum 的递归过程,执行整数 1 到 n 的加法,其中 n 是通过 ECX 传递的输入参数。CalcSum 用 EAX 返回和数:
;整数求和 (RecursiveSum. asm) INCLUDE Irvine32.inc .code main PROC mov ecx,5 ; 计数值 = 5 mov eax,0 ; 保存和数 call CalcSum ; 计算和数 L1: call WriteDec ; 显示 EAX call Crlf ; 换行 exit main ENDP ;-------------------------------------------------------- CalcSum PROC ; 计算整数列表的和数 ; 接收: ECX = 计数值 ; 返回: EAX = 和数 ;-------------------------------------------------------- cmp ecx,0 ; 检查计数值 jz L2 ; 若为零则推出 add eax,ecx ; 否则,与和数相加 dec ecx ; 计数值递减 call CalcSum ; 递归调用 L2: ret CalcSum ENDP END MainCalcSum 的开始两行检查计数值,若 ECX=0 则退出该过程,代码就跳过了后续的递归调用。当第一次执行 RET 指令时,它返回到前一次对 CalcSum 的调用,而这个调用再返回到它的前一次调用,依序前推。
下表给出了 CALL 指令压入堆栈的返回地址(用标号表示),以及与之相应的 ECX(计数值)和 EAX(和数)的值。
入栈的返回地址 ECX的值 EAX的值 入栈的返回地址 ECX的值 EAX的值 L1 5 0 L2 2 12 L2 4 5 L2 1 14 L2 3 9 L2 0 15 即使是一个简单的递归过程也会使用大量的堆栈空间。每次过程调用发生时最少占用 4 字节的堆栈空间,因为要把返回地址保存到堆栈。
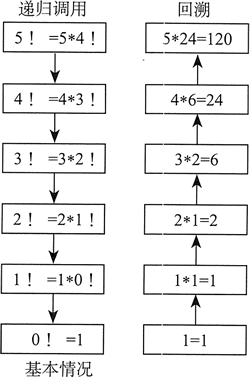
计算阶乘
递归子程序经常用堆栈参数来保存临时数据。当递归调用展开时,保存在堆栈中的数据就有用了。下面要查看的例子是计算整数 n 的阶乘。阶乘算法计算 n!,其中 n 是无符号整数。第一次调用 factorial 函数时,参数 n 就是初始数字。下面给出的是用 C/C++/Java 语法编写的代码:
int function factorial(int n) { if(n == 0) return 1; else return n * factorial(n-1); }假设给定任意 n,即可计算 n-1 的阶乘。这样就可以不断减少 n,直到它等于 0 为止。根据定义,0!=l。而回溯到原始表达式 n! 的过程,就会累积每次的乘积。比如计算 5! 的递归算法如下图所示,左列为算法递进过程,右列为算法回溯过程。